rtl_designs
Binary to Gray Converter
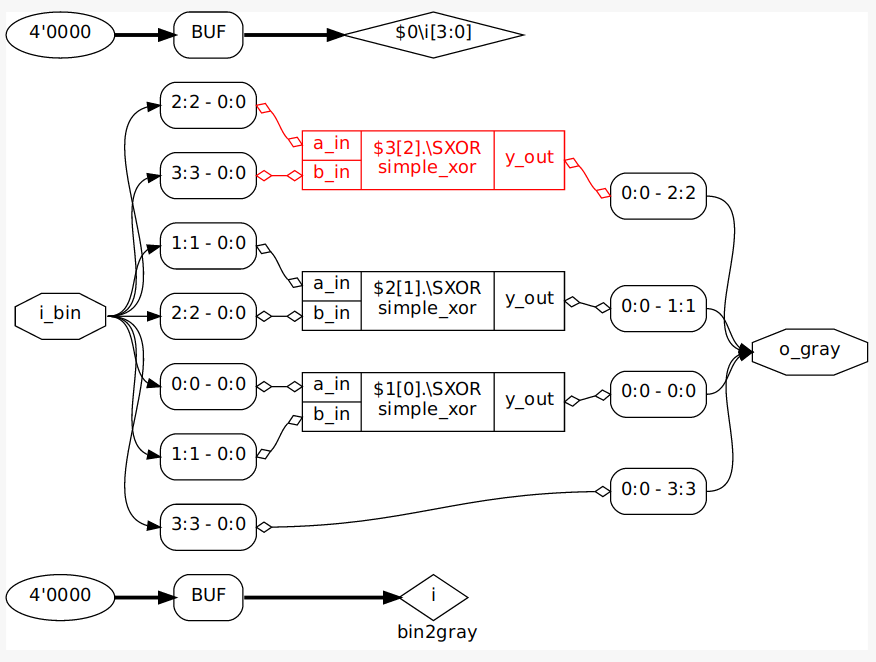
A custom binary to gray counter. For simplicity, I shall be designing a 4-bit binary to gray converter and verify it.
Note: The parameter LEN can be adjusted to construct a n-bit binary to gray code
converter.
Gray code was introduced to resolve the major problem with the natural binary code.
Consider the transition between 011 to 100 (i.e 3 to 4) where every bits are
changing, there is a possible of appearing false states while receiving 100. This
problem can be solved by changing only one switch at a time, so there is never
ambiguity of position. These are also known as unit-distance, single distance,
single-step, monostrophic, or syncopic codes. (more)
Truth table of 4-bit Binary to Gray Code:

Equations:
G0 = B0 ^ B1
G1 = B1 ^ B2
G2 = B2 ^ B3
G3 = B3
Verified Results:
2.00ns --------------------------------------
2.00ns | Inc Test 4Bit
2.00ns --------------------------------------
4.00ns Binary: 0110 | Exp: 0101 | Gray: 0101
6.00ns Binary: 1101 | Exp: 1011 | Gray: 1011
8.00ns Binary: 0110 | Exp: 0101 | Gray: 0101
0.00ns Binary: 1010 | Exp: 1111 | Gray: 1111
2.00ns Binary: 1011 | Exp: 1110 | Gray: 1110
4.00ns Binary: 1010 | Exp: 1111 | Gray: 1111
6.00ns Binary: 0001 | Exp: 0001 | Gray: 0001
8.00ns Binary: 0100 | Exp: 0110 | Gray: 0110
8.00ns --------------------------------------
8.00ns inc_test4b passed
8.00ns
*********************************************************************************
** TEST STATUS SIM TIME (ns) REAL TIME (s) RATIO (ns/s) **
**************************************************************************************
** tb_bin2gray.basic_test PASS 2.00 0.00 1213.53 **
** tb_bin2gray.inc_test4b PASS 16.00 0.00 6633.69 **
**************************************************************************************
** TESTS=2 PASS=2 FAIL=0 SKIP=0 18.00 0.46 39.37 **
**************************************************************************************